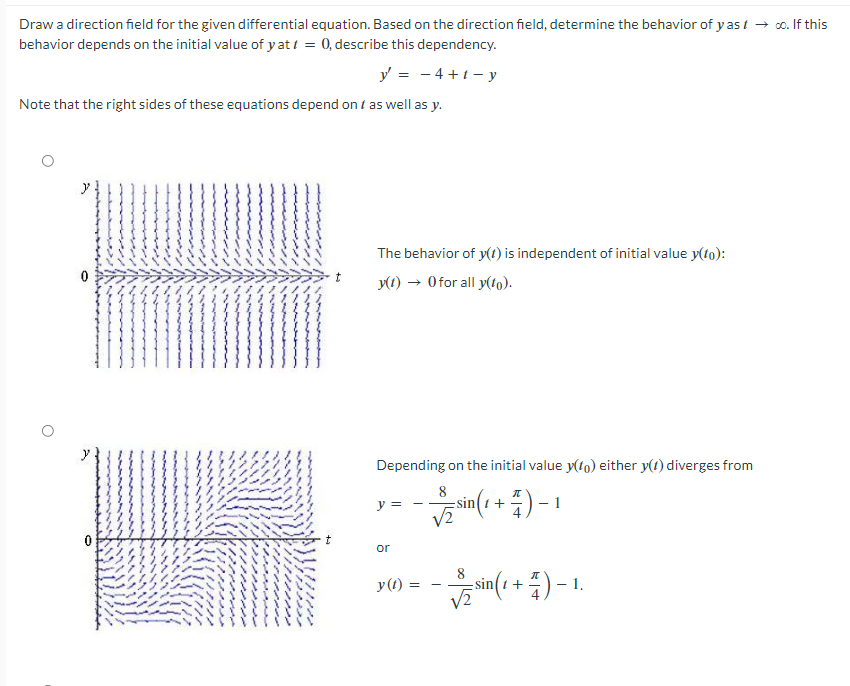
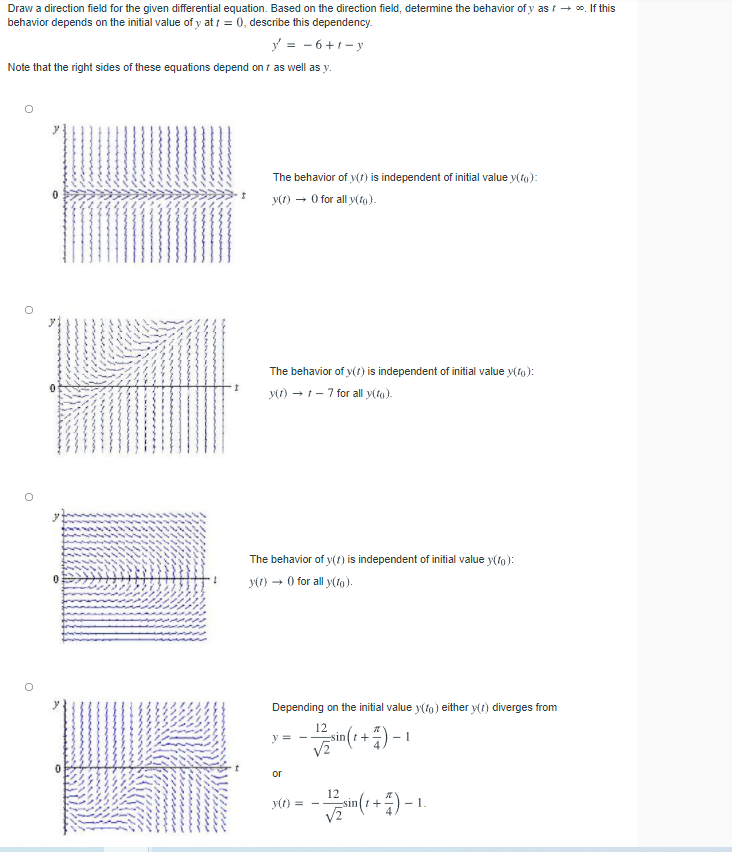
Draw A Direction Field For The Given Differential Equation
Draw A Direction Field For The Given Differential Equation - For a differential equation in this form, we’ll sketch the direction field by using a set of coordinate pairs ???(x,y)??? And one of those is in the. We also investigate how direction fields can be used to determine some information about the solution to a differential equation without actually having the solution. Web draw a direction field for the given differential equations and use this direction field to determine the behavior of y as t → ∞. Web to create a direction field, we start with the first equation: Based on an inspection of the direction field, describe how solutions behave for large t. In each of problems 7 through 10, draw a direction field for the given differential equation. \ ( y=0\) is a stable equilibrium and \ ( y=2\) is unstable. Dy dx =x2cosx d y d x = x 2 cos x 12. Web as you’ll see, the combination of direction fields and integral curves gives useful insights into the behavior of the solutions of the differential equation even if we can’t obtain exact solutions. First of all , find the points where derivati. At each point in a direction field, a line segment appears whose slope is equal to the slope of a solution to the differential equation passing through that point. \ ( y=0\) is a stable equilibrium and \ ( y=2\) is unstable. O diverge converge for y 2 0, diverge for. For a differential equation in this form, we’ll sketch the direction field by using a set of coordinate pairs ???(x,y)??? Web draw a direction field for the given differential equation. We’ll study numerical methods for solving a single first order equation equation 1.3.1 1.3.1 in chapter 3. Based on the direction field, determine the behavior of y as t →.. We’ll study numerical methods for solving a single first order equation equation 1.3.1 1.3.1 in chapter 3. Y′ =et y ′ = e t show solution 11. When the direction field is shown, click on the initial point to sketch the graph of the solution passing through the point. Web (1) click show direction field to sketch the direction field. Dy dx =x2cosx d y d x = x 2 cos x 12. Web in this section we discuss direction fields and how to sketch them. At each point in a direction field, a line segment appears whose slope is equal to the slope of a solution to the differential equation passing through that point. Find the general solution of. Based on an inspection of the direction field, describe how solutions behave for large t. Draw your solution on top of the direction field. O diverge converge for y 2 0, diverge for y this problem has been solved! Graph functions, plot points, visualize algebraic equations, add sliders, animate graphs, and more. Y =t3 y ′ = t 3 10. Drag the initial point to move it to a different location. View the full answer transcribed image text: Web as you’ll see, the combination of direction fields and integral curves gives useful insights into the behavior of the solutions of the differential equation even if we can’t obtain exact solutions. Y′ =et y ′ = e t show solution 11.. Web draw the direction field for the following differential equations, then solve the differential equation. For a differential equation in this form, we’ll sketch the direction field by using a set of coordinate pairs ???(x,y)??? 9) \( y'=t^3\) 10) \( y'=e^t\) answer. Based on an inspection of the direction field, describe how solutions behave for large t. We’ll study numerical. Web a direction field (or slope field / vector field) is a picture of the general solution to a first order differential equation with the form edit the gradient function in the input box at the top. Based on the direction field, determine the behavior of y as t →. Y′ =et y ′ = e t show solution 11.. O diverge converge for y 2 0, diverge for y this problem has been solved! Based on the direction field, determine the behavior of y as t →. Web as you’ll see, the combination of direction fields and integral curves gives useful insights into the behavior of the solutions of the differential equation even if we can’t obtain exact solutions.. And one of those is in the. Dy dt = tet d y d t = t e t Graph functions, plot points, visualize algebraic equations, add sliders, animate graphs, and more. Sketch 5 isoclines per differential equation (show all work). Web in this section we discuss direction fields and how to sketch them. \ ( y=0\) is a stable equilibrium and \ ( y=2\) is unstable. Does your solution follow along the arrows on your direction field? Web a direction field (or slope field / vector field) is a picture of the general solution to a first order differential equation with the form edit the gradient function in the input box at the top. Draw your solution on top of the direction field. Web draw a direction field for the given differential equation. Drag the initial point to move it to a different location. Web create a direction field for the differential equation y ′ = (x + 5) (y + 2) (y 2 − 4 y + 4) y ′ = (x + 5) (y + 2) (y 2 − 4 y + 4) and identify any equilibrium solutions. Based on the direction field, determine the behavior of y as t →. First of all , find the points where derivati. When the direction field is shown, click on the initial point to sketch the graph of the solution passing through the point. Y =t3 y ′ = t 3 10. For a differential equation in this form, we’ll sketch the direction field by using a set of coordinate pairs ???(x,y)??? Graph functions, plot points, visualize algebraic equations, add sliders, animate graphs, and more. We’ll study numerical methods for solving a single first order equation equation 1.3.1 1.3.1 in chapter 3. Web as you’ll see, the combination of direction fields and integral curves gives useful insights into the behavior of the solutions of the differential equation even if we can’t obtain exact solutions. 9) \( y'=t^3\) 10) \( y'=e^t\) answer.
Differential Equations Direction Fields Example 1 YouTube

Differential Equations Direction Fields YouTube

Solved 1. Draw a direction field for the given differential
Solved Draw a direction field for the given differential
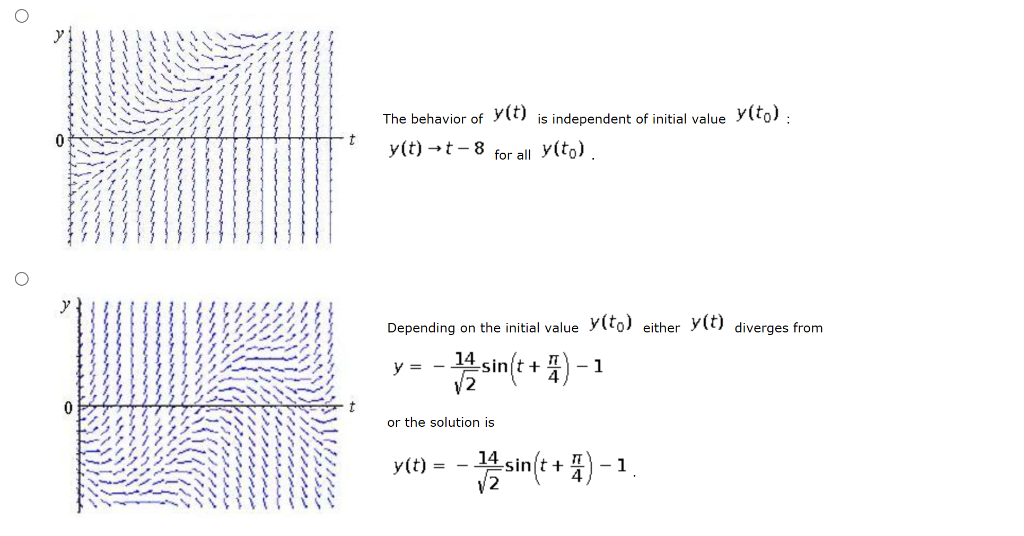
Solved Draw a direction field for the given differential
Solved Draw a direction field for the given differential
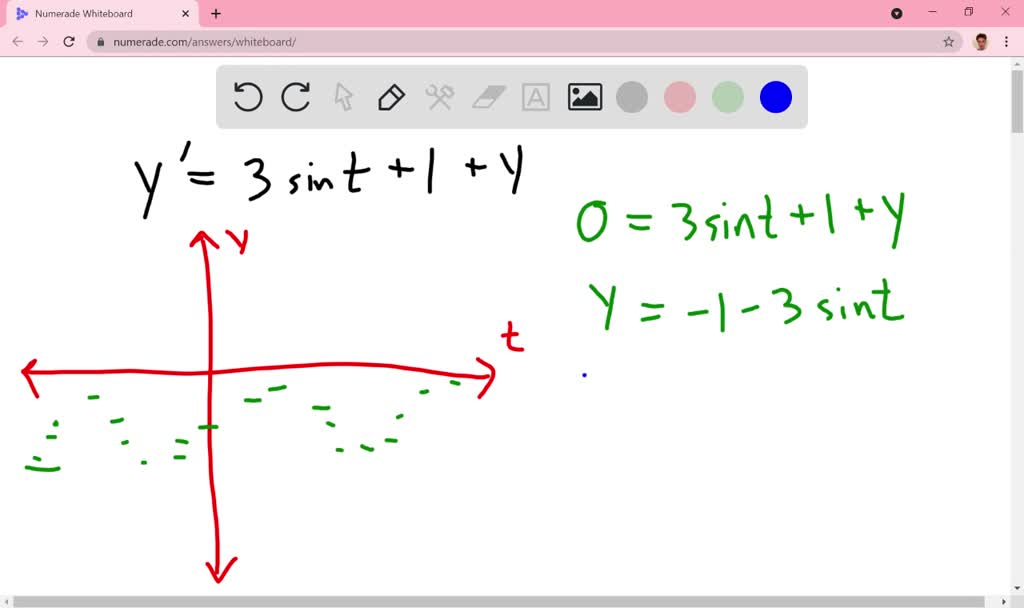
SOLVEDdraw a direction field for the given differential equation
Solved Draw a direction field for the given differential
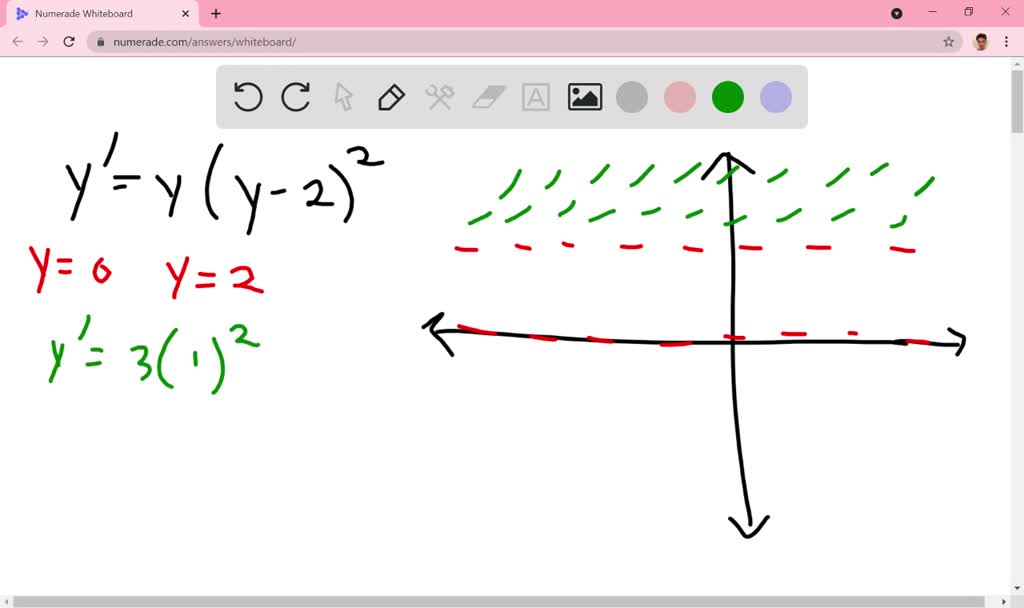
SOLVEDdraw a direction field for the given differential equation

(a) Draw a direction field for the given differential… SolvedLib
O Diverge Converge For Y 2 0, Diverge For Y This Problem Has Been Solved!
Does Your Solution Follow Along The Arrows On Your Direction Field?
If This Behavior Depends On The Initial Value Of Y At T = 0, Describe This Dependency.
Dy Dx =X2Cosx D Y D X = X 2 Cos X 12.
Related Post: