Draw A Fibonacci Spiral
Draw A Fibonacci Spiral - You get the next one. You'll need to draw a system of squares that will end up inscribing the spiral, acting as. Web how to draw a fibonacci spiral. 360/13=27.69, and marked the degrees around the circle. The main principle of using the fibonacci spiral in technical analysis is setting the first radius as the distance between two significant extremum points of chart. The whorls spiral out in the fibonacci sequence. Web fibonacci spiral is created by drawing circular arcs connecting the opposit corners of squares in the fibonacci tiling, thus the radius grows proportionally to fibonacci ratio. Web although it may not appear to be clear, there is a strong link between this sequence of numbers and artwork composition. The fibonacci sequence (1, 1, 2, 3, 5, 8, 13.) dictates the size of the squares that are used to draw the arcs. The function can use the current value for the fibonacci number as the arc radius. Trace the squares from corner to corner across the diagonal. Web fibonacci spiral is created by drawing circular arcs connecting the opposit corners of squares in the fibonacci tiling, thus the radius grows proportionally to fibonacci ratio. Web kathie huff 114 subscribers subscribe like share 14k views 6 years ago talks students through the process to make a fibonacci spiral. The arcs are drawn in the images for the squares using random dots that paint the arc line. Fibonacci numbers are strongly related to the golden ratio: Web here is an eight armed fibonacci spiral. Graph functions, plot points, visualize algebraic equations, add sliders, animate graphs, and more. Learn how to construct the fibonacci spiral using the fibonacci sequence. Web if you were to draw a line starting in the right bottom corner of a golden rectangle within the first square and then touch each succeeding multiple squares outside corners, you would create a fibonacci spiral. These drawings are actually a close approximation of the patterns we see in nature as an exact replication is not possible. The fibonacci. Fibonacci numbers are strongly related to the golden ratio: The fibonacci sequence (1, 1, 2, 3, 5, 8, 13.) dictates the size of the squares that are used to draw the arcs. You will need paper, pencil, a. Graph functions, plot points, visualize algebraic equations, add sliders, animate graphs, and more. The plant kingdom this pattern of numbers can be. Learn how to construct the fibonacci spiral using the fibonacci sequence. Thanks to vihart and her awesome. The fibonacci sequence continues indefinitely. Web full method 1. Web instructions make squares with sides that correspond to the numbers in the fibonacci sequence. Web so, 1 + 1 = 2, 1 + 2 = 3, 2 + 3 = 5 and so on. This works by adding the two previous numbers: The fibonacci sequence (1, 1, 2, 3, 5, 8, 13.) dictates the size of the squares that are used to draw the arcs. 360/13=27.69, and marked the degrees around the circle. Sunflower. Now you can draw the spiral. Web how to draw a fibonacci spiral how to construct fibonacci spiral (golden spiral) with compass. Draw each of these squares. Web explore math with our beautiful, free online graphing calculator. Fibonacci numbers are strongly related to the golden ratio: The arcs are drawn in the images for the squares using random dots that paint the arc line. Every new square should be shifted in. You'll need to draw a system of squares that will end up inscribing the spiral, acting as. You get the next one. The fibonacci spiral may be created by seeing each number as a square. It follows the rotation sequence to know the direction to draw the arc. The main principle of using the fibonacci spiral in technical analysis is setting the first radius as the distance between two significant extremum points of chart. Web we can add a fibonacci spiral to the squares in the program above using a function to draw arcs. Web. You'll need to draw a system of squares that will end up inscribing the spiral, acting as. Draw each of these squares. 360/13=27.69, and marked the degrees around the circle. The fibonacci spiral may be created by seeing each number as a square (growing in size with the sequence) and connecting the opposing corners of each square. Draw squares using. The arcs are drawn in the images for the squares using random dots that paint the arc line. Web the fibonacci spiral is a geometrical pattern that is derived from the fibonacci sequence. A golden spiral with initial radius 1 is the locus of points of polar coordinates satisfying where is the golden ratio. These can be found many places in nature as well.materials: It follows the rotation sequence to know the direction to draw the arc. Every new square should be shifted in. The fibonacci spiral may be created by seeing each number as a square (growing in size with the sequence) and connecting the opposing corners of each square. Web instructions make squares with sides that correspond to the numbers in the fibonacci sequence. You'll need to draw a system of squares that will end up inscribing the spiral, acting as. Learn how to construct the fibonacci spiral using the fibonacci sequence. Web how to draw a fibonacci spiral. Web we can add a fibonacci spiral to the squares in the program above using a function to draw arcs. The function can use the current value for the fibonacci number as the arc radius. The plant kingdom this pattern of numbers can be seen in nature. The fibonacci sequence (1, 1, 2, 3, 5, 8, 13.) dictates the size of the squares that are used to draw the arcs. Draw each of these squares.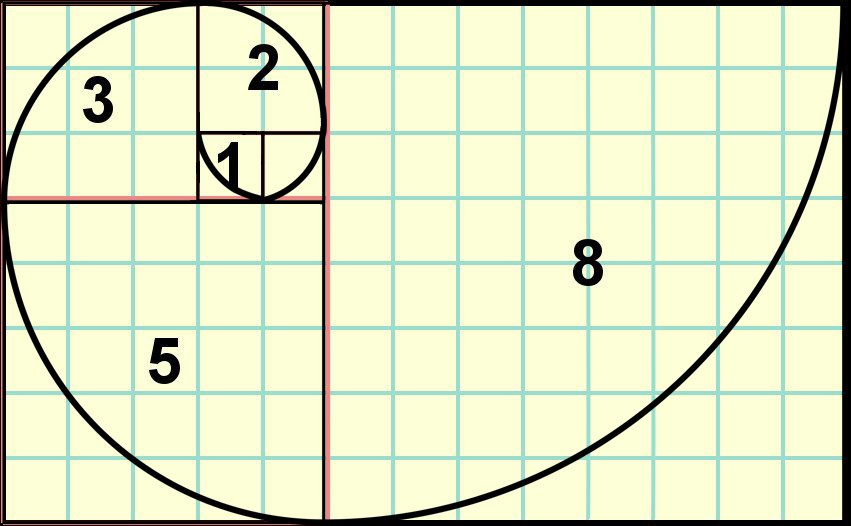
Fibonacci Hwa Eubanks

How To Draw Fibonacci Sequence at How To Draw
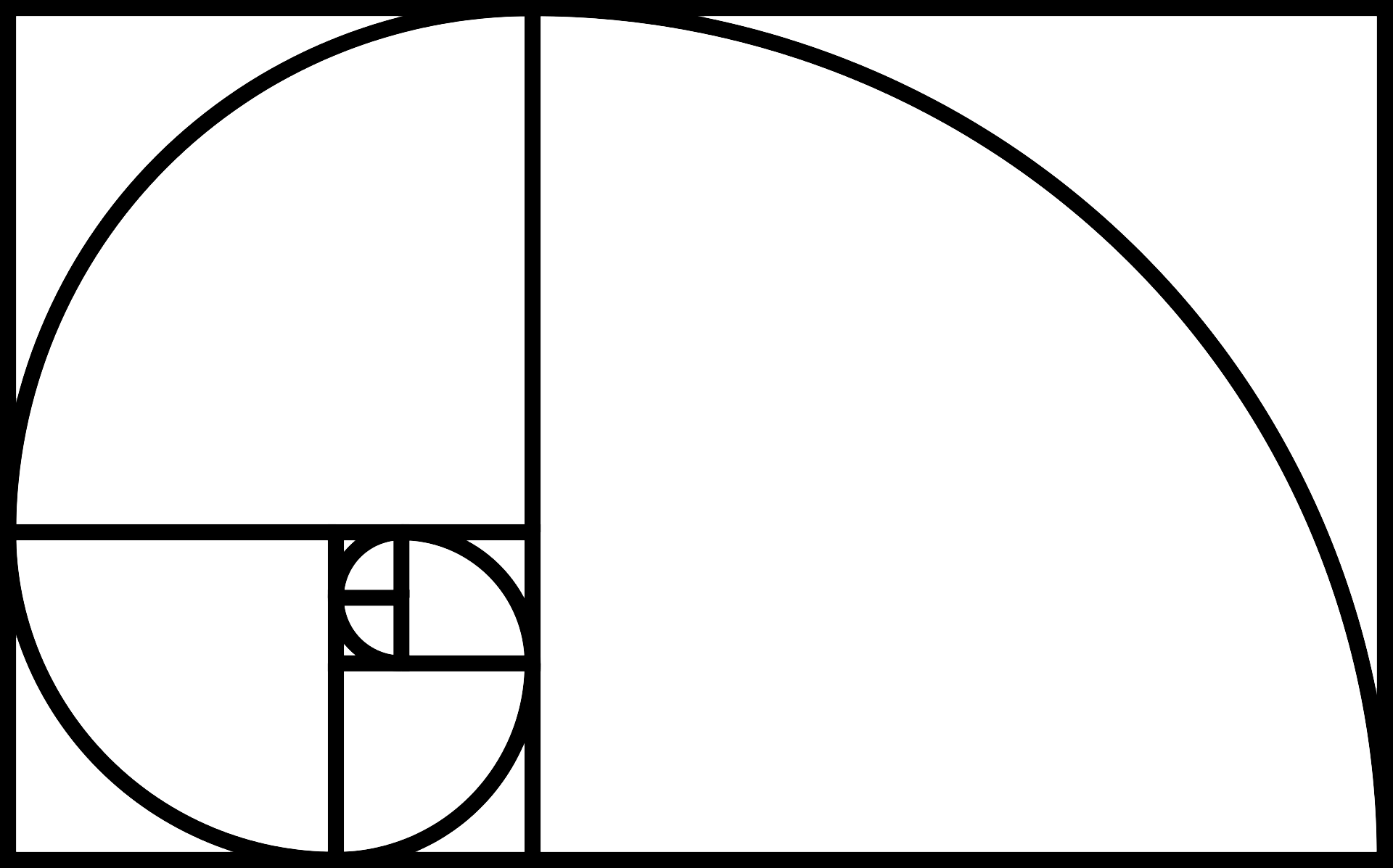
The Golden Ratio/Fibonacci Sequence What It Means to Photographers

How To Draw Fibonacci Sequence at How To Draw

How To Draw Fibonacci Sequence at How To Draw

How to Draw the Golden Spiral 13 Steps (with Pictures) wikiHow

FileFibonacci Spiral GeoGebra.svg Wikipedia

How To Draw Fibonacci Sequence at How To Draw
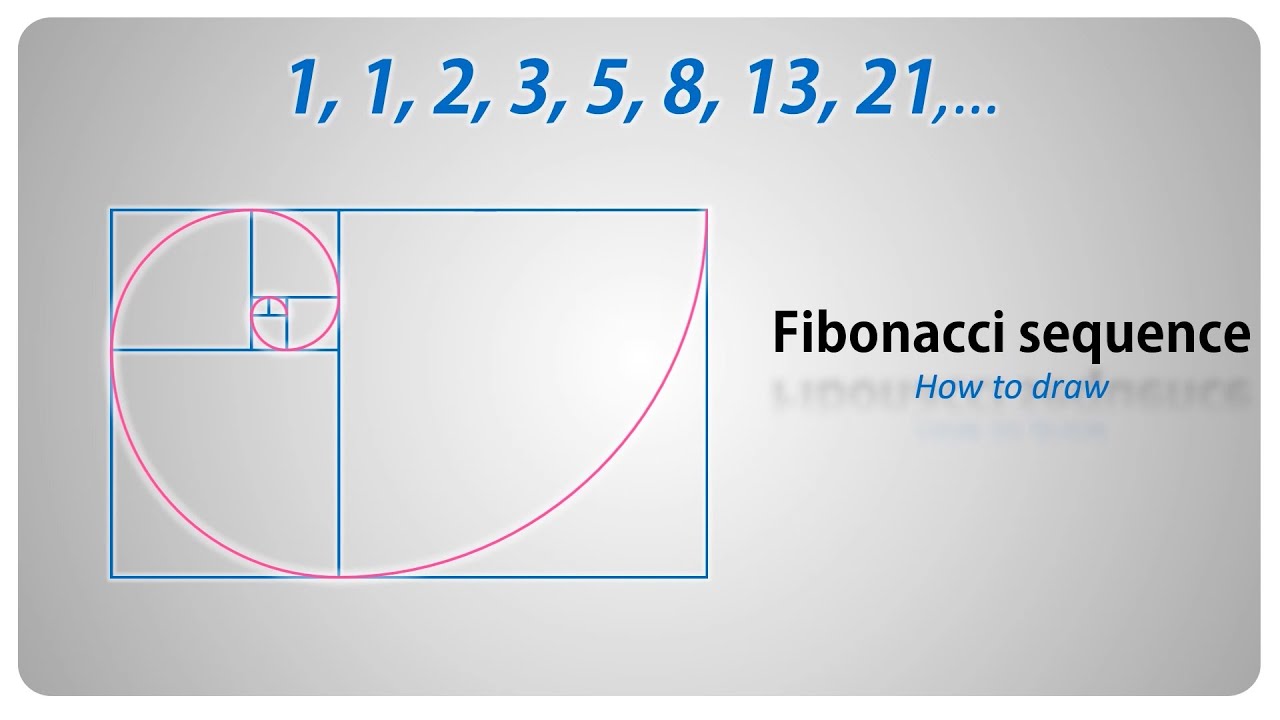
How to draw the Fibonacci sequence / golden spiral step by step

How To Draw A Fibonacci Spiral Youtube The ultimate guide
You Get The Next One.
These Drawings Are Actually A Close Approximation Of The Patterns We See In Nature As An Exact Replication Is Not Possible.
Using This Approach, We Can Successively Calculate Fn For As Many Generations As We Like.
Graph Functions, Plot Points, Visualize Algebraic Equations, Add Sliders, Animate Graphs, And More.
Related Post: