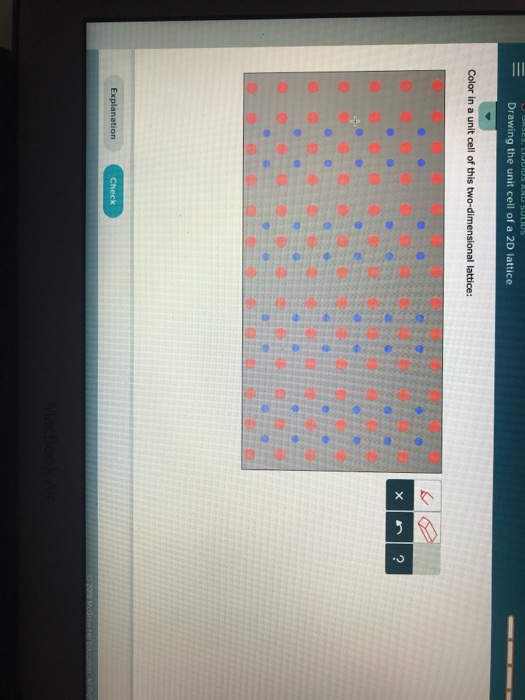
Drawing The Unit Cell Of A 2D Lattice Aleks
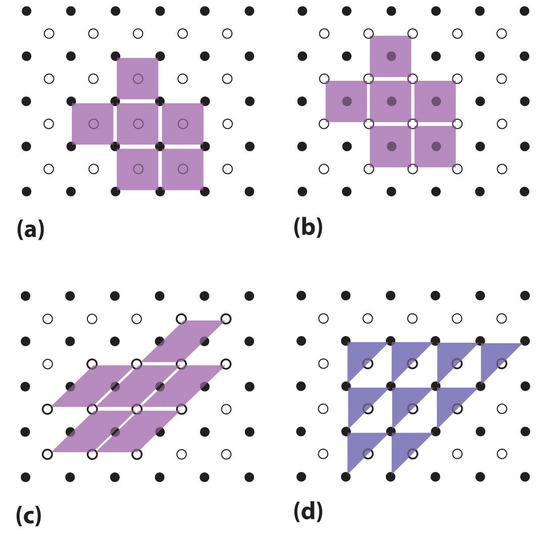
Drawing The Unit Cell Of A 2D Lattice Aleks - This topic deals with lattice and its characteristics. Primitive unit cells contain one lattice point only. This small portion when repeated can generate the whole lattice and is. Web meshes are 2d arrays of lattice points, lattices are 3d arrays. Web the reciprocal lattice just like we can define a real space lattice in terms of our real space lattice vectors, we can define a reciprocal space lattice in terms of our reciprocal space lattice vectors: This structure contains sulfide ions on the lattice points of an fcc lattice. Web drawing the unit cell of a 2d lattice this problem has been solved! You'll get a detailed solution from a subject matter expert that helps you learn core concepts. Web atoms on a corner are shared by eight unit cells and hence contribute only 1 8 atom per unit cell, giving 8× 1 8 =1 au atom per unit cell. In this class we will only focus on the cubic unit cell, and there are three types of cubic cells that you need to be familiar with, and these are represented in figure 12.1.b. Web the cubic form of zinc sulfide, zinc blende, also crystallizes in an fcc unit cell, as illustrated in figure 10.61. The crystal basis is defined by Web our videos prepare you to succeed in your college classes. So, the unit cell of this 2d lattice is a square. A lattice can be described in terms of unit cell and. A lattice can be described in terms of unit cell and lattice parameters (constants): Web a periodic array of “dots” (or lattice points) with infinite repetition. Web our videos prepare you to succeed in your college classes. Let us help you simplify your studying. (a, b, c) and (α, β, γ). This small portion when repeated can generate the whole lattice and is. Primitive unit cells contain one lattice point only. Web the cubic form of zinc sulfide, zinc blende, also crystallizes in an fcc unit cell, as illustrated in figure 10.61. The conventional primitive unit cell has the shortest and most nearly equal lattice vectors bounding it. You'll get a. Web our videos prepare you to succeed in your college classes. (a, b, c) and (α, β, γ). If you are having trouble with chemistry, organic, physics, calculus, or statistics, we got your back! You'll get a detailed solution from a subject matter expert that helps you learn core concepts. A lattice is the best way to explain the periodic. Web unit cell in two dimensional and three dimensional lattices. Web the reciprocal lattice just like we can define a real space lattice in terms of our real space lattice vectors, we can define a reciprocal space lattice in terms of our reciprocal space lattice vectors: In this case, the repeating pattern is a square. Web there are 7 types. Recognizing and naming lattices with cubic unit cells. Web about press copyright contact us creators advertise developers terms privacy policy & safety how youtube works press copyright contact us creators advertise. Web the reciprocal lattice just like we can define a real space lattice in terms of our real space lattice vectors, we can define a reciprocal space lattice in. So, the unit cell of this 2d lattice is a square. Web about press copyright contact us creators advertise developers terms privacy policy & safety how youtube works test new features nfl sunday ticket press copyright. This topic deals with lattice and its characteristics. Web meshes are 2d arrays of lattice points, lattices are 3d arrays. R d ha kb. The total number of au atoms in each unit cell is thus 3 + 1 = 4. Web the cubic form of zinc sulfide, zinc blende, also crystallizes in an fcc unit cell, as illustrated in figure 10.61. In this class we will only focus on the cubic unit cell, and there are three types of cubic cells that you. Unit cells can be used to build the entire lattice. Our videos will help you understand concepts, solve your homework, and do great on your exams. Consequently, unit cell axes join points with identical environments. In this class we will only focus on the cubic unit cell, and there are three types of cubic cells that you need to be. Web our videos prepare you to succeed in your college classes. A lattice is the best way to explain the periodic structure of an ideal crystal. So, the unit cell of this 2d lattice is a square. This problem has been solved! Web we describe the shapes of unit cells with unit cell parameters that include a, b, and c,. The total number of au atoms in each unit cell is thus 3 + 1 = 4. Recognizing and naming lattices with cubic unit cells. Web our videos prepare you to succeed in your college classes. A lattice can be described in terms of unit cell and lattice parameters (constants): You'll get a detailed solution from a subject matter expert that helps you learn core concepts. A lattice is the best way to explain the periodic structure of an ideal crystal. You'll get a detailed solution from a subject matter expert that helps you learn core concepts. Let us help you simplify your studying. The crystal basis is defined by In reality, we have to deal with finite sizes. This structure contains sulfide ions on the lattice points of an fcc lattice. The conventional primitive unit cell has the shortest and most nearly equal lattice vectors bounding it. Web the reciprocal lattice just like we can define a real space lattice in terms of our real space lattice vectors, we can define a reciprocal space lattice in terms of our reciprocal space lattice vectors: Web the cubic form of zinc sulfide, zinc blende, also crystallizes in an fcc unit cell, as illustrated in figure 10.61. R d ha kb lc hkl * * the real and reciprocal space lattice vectors form an orthonormal set: Web atoms on a corner are shared by eight unit cells and hence contribute only 1 8 atom per unit cell, giving 8× 1 8 =1 au atom per unit cell.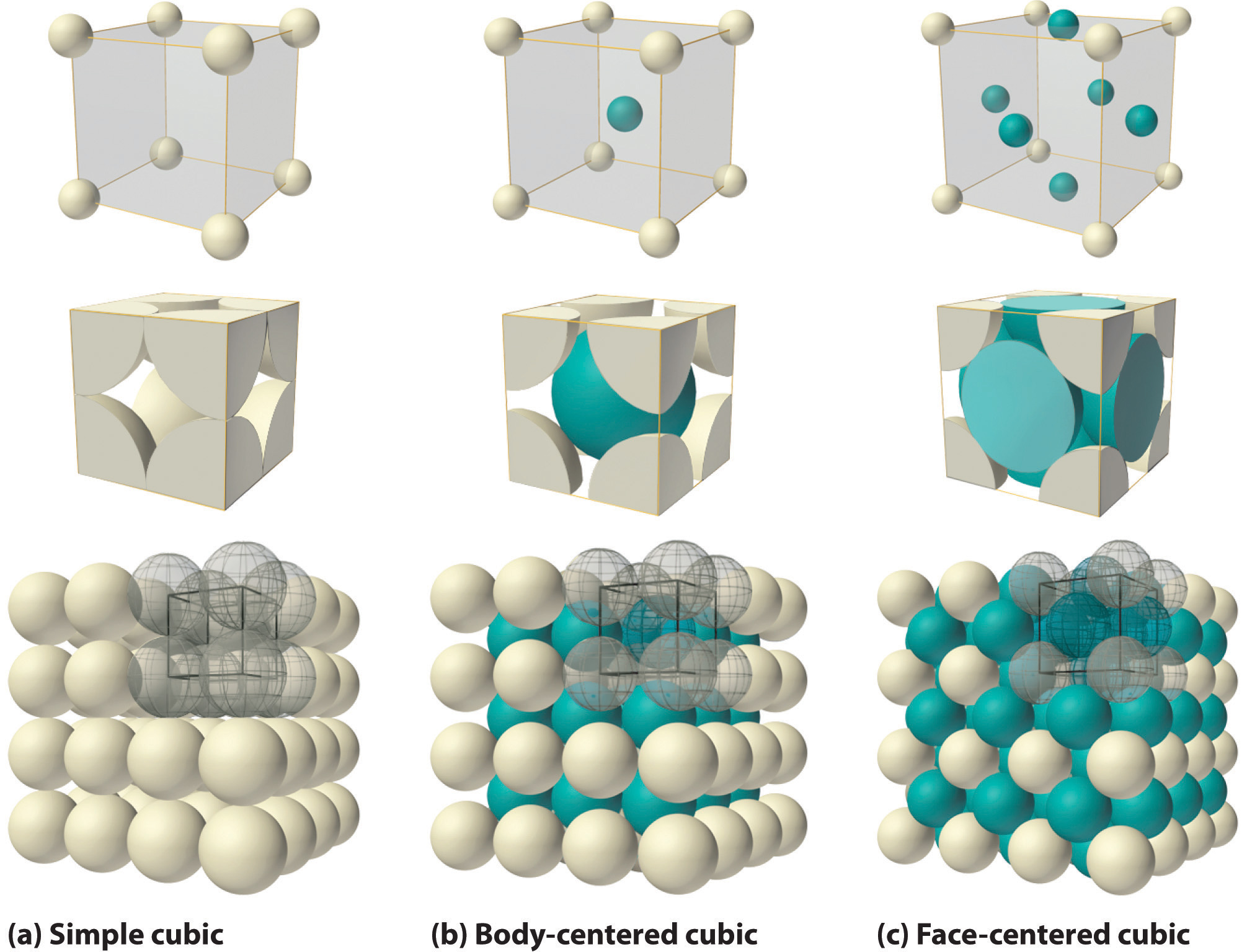
12.1 Crystal Lattices and Unit Cells Chemistry LibreTexts
10.3 Lattices and Unit Cells Chemistry LibreTexts
Drawing the Unit Cell of a 2d Lattice

The 2D periodic material (a) geometry, (b) 2D lattice, (c) unit cell

2D lattice made of framelike diamondsquare unit cells. a Lattice. b
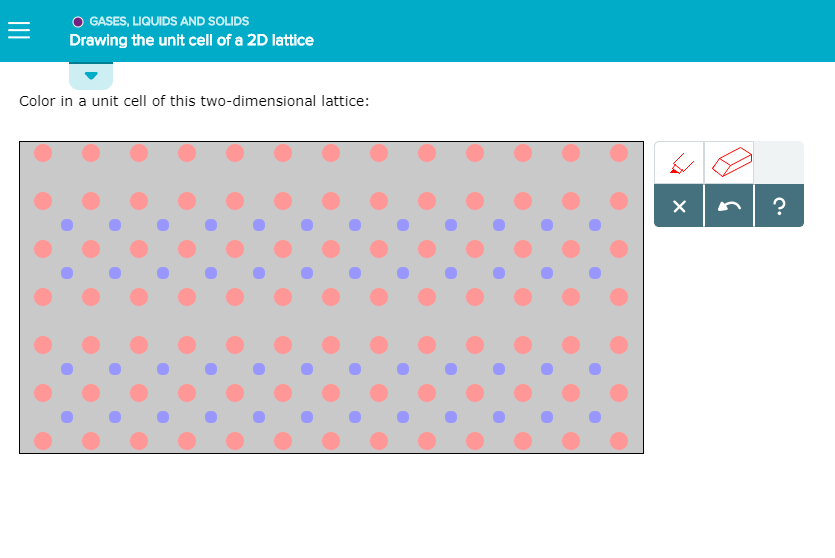
Drawing the Unit Cell of a 2d Lattice

Drawing the Unit Cell of a 2d Lattice

Lattice structure of a unit cell with a face cubic centered (fcc

Diagrams of (a) a regular 2D network showing the unit cell for lattice
Solved Drawing the unit cell of a 2D lattice
By Convention, The Angle Between The A And B Edges Is Γ ( C In The Greek Alphabet), The Angle Between A And C Is Β ( B In The Greek Alphabet), And The Angle Between B And C.
Web About Press Copyright Contact Us Creators Advertise Developers Terms Privacy Policy & Safety How Youtube Works Press Copyright Contact Us Creators Advertise.
(A, B, C) And (Α, Β, Γ).
This Problem Has Been Solved!
Related Post: