How To Draw Vector Fields
How To Draw Vector Fields - We can now represent a vector field in terms of its components of functions or unit vectors, but representing it visually by sketching it is more complex because the domain of a vector field is in [latex]\mathbb{r}^2[/latex], as is the range. So to start off, let's take a very simple example, one where the vector that outputs is. →f (x,y) =−y→i +x→j f → ( x, y) = − y i → + x j →. Then, we would draw vector 〈3, 1〉 at point (4, −1). →f (x,y,z) =2x→i −2y→j −2x→k f → ( x, y, z) = 2 x i → − 2 y j → − 2. A) is the vector fieldf⃗(x,y) = xy x2 a gradient field? Web vector fields use the same amount of input dimensions as a graph, but instead of creating new dimensions for each output like a graph does, they condense the outputs into a single vector. After an example, four exercises are given and detailed solutions are provided. Web in both cases, draw a contour map of f and use gradients to draw the vector field⃗f(x,y) = ∇f. Example 1 sketch each of the following vector fields. After an example, four exercises are given and detailed solutions are provided. A vector field \(\vecs{f}\) is called conservative if there exists a scalar function \(f\) such that \(\vecs \nabla f=\vecs{f}\). Web the easiest way to make sense of the vector field model is using velocity (first derivative, output) and location, with the model of the fluid flow. We know. Vector fields exhibit certain common shapes, which include a source (where the vectors emanate out of one point), a sink (where the vectors disappear into a hole, something. A vector field \(\vecs{f}\) is called conservative if there exists a scalar function \(f\) such that \(\vecs \nabla f=\vecs{f}\). Find a function f(x,y) such that f⃗ = ∇f. Then, we would draw. Web the easiest way to make sense of the vector field model is using velocity (first derivative, output) and location, with the model of the fluid flow. →f (x,y,z) =2x→i −2y→j −2x→k f → ( x, y, z) = 2 x i → − 2 y j → − 2. Example 1 sketch each of the following vector fields. Web. A vector field \(\vecs{f}\) is called conservative if there exists a scalar function \(f\) such that \(\vecs \nabla f=\vecs{f}\). Web explore math with our beautiful, free online graphing calculator. Web the easiest way to make sense of the vector field model is using velocity (first derivative, output) and location, with the model of the fluid flow. A) is the vector. →f (x,y) =−y→i +x→j f → ( x, y) = − y i → + x j →. Web in this video we will define the concept of a vector field, talk about some basic terminology, practice drawing vector fields by hand and then turn to the technology to plot vector fields on the. Graph functions, plot points, visualize algebraic. Web let e be a set in r 3. In this case, since we divided by $z$, the magnitude of the vector field decreases as $z$ increases. These are like functions that take in coordinates and give. F → ( x, y, z) = p ( x, y, z), q ( x, y, z), r ( x, y, z) where. Graph functions, plot points, visualize algebraic equations, add sliders, animate graphs, and more. In this case, since we divided by $z$, the magnitude of the vector field decreases as $z$ increases. A vector field is simply a diagram that shows the magnitude and direction of vectors (forces, velocities, etc) in different parts of space. Vector fields exhibit certain common shapes,. Vector fields and line integrals in the plane. Web we can sketch a vector field by examining its defining equation to determine relative magnitudes in various locations and then drawing enough vectors to determine a pattern. Vector fields exhibit certain common shapes, which include a source (where the vectors emanate out of one point), a sink (where the vectors disappear. A vector field is simply a diagram that shows the magnitude and direction of vectors (forces, velocities, etc) in different parts of space. A) is the vector fieldf⃗(x,y) = xy x2 a gradient field? Web let e be a set in r 3. In this case, since we divided by $z$, the magnitude of the vector field decreases as $z$. Web this video aims to help you practise sketching vector fields in two dimensions. Vector fields and line integrals in the plane. A vector function is a function that takes a number of inputs, and returns a vector. A vector field \(\vecs{f}\) is called conservative if there exists a scalar function \(f\) such that \(\vecs \nabla f=\vecs{f}\). Example 1 sketch. Web explore math with our beautiful, free online graphing calculator. To do this, draw the vector associated with a given point at the point in a plane. A vector function is a function that takes a number of inputs, and returns a vector. Web this video aims to help you practise sketching vector fields in two dimensions. After an example, four exercises are given and detailed solutions are provided. For example, suppose the vector associated with point (4, −1) is 〈3, 1〉. Web in this video we will define the concept of a vector field, talk about some basic terminology, practice drawing vector fields by hand and then turn to the technology to plot vector fields on the. Example 1 sketch each of the following vector fields. The vector field f⃗(x,y) = x (x2+y2)(3/2) y (x 2+y )(3/2) # appears in electrostatics. These are like functions that take in coordinates and give. And you draw that vector off of the point itself. Web let e be a set in r 3. Web drawing a vector field. Before we learn how to draw more vector fields, let us first show you how to find a vector associated with a given point. Web we can sketch a vector field by examining its defining equation to determine relative magnitudes in various locations and then drawing enough vectors to determine a pattern. An interactive visulization of vector fields.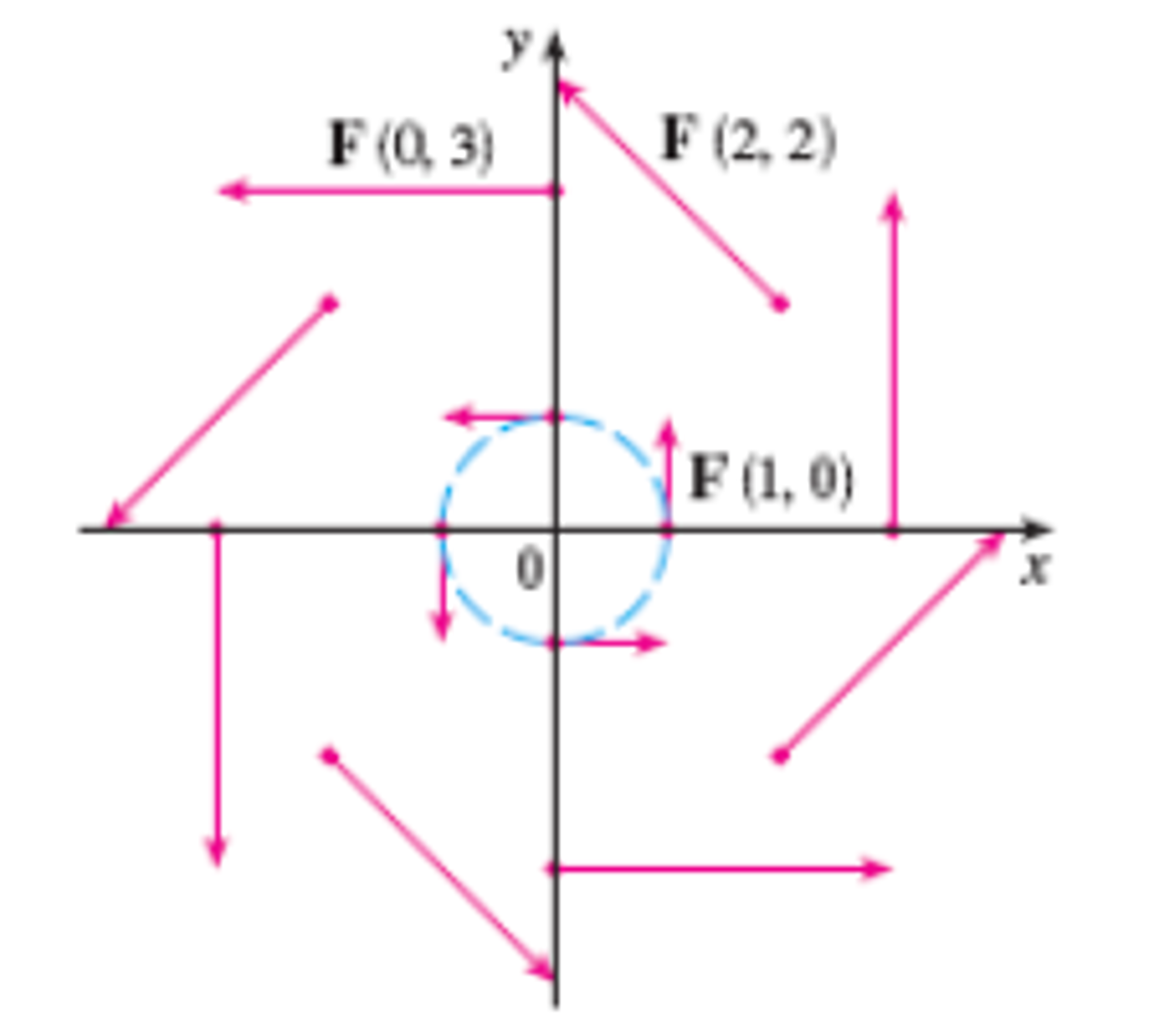
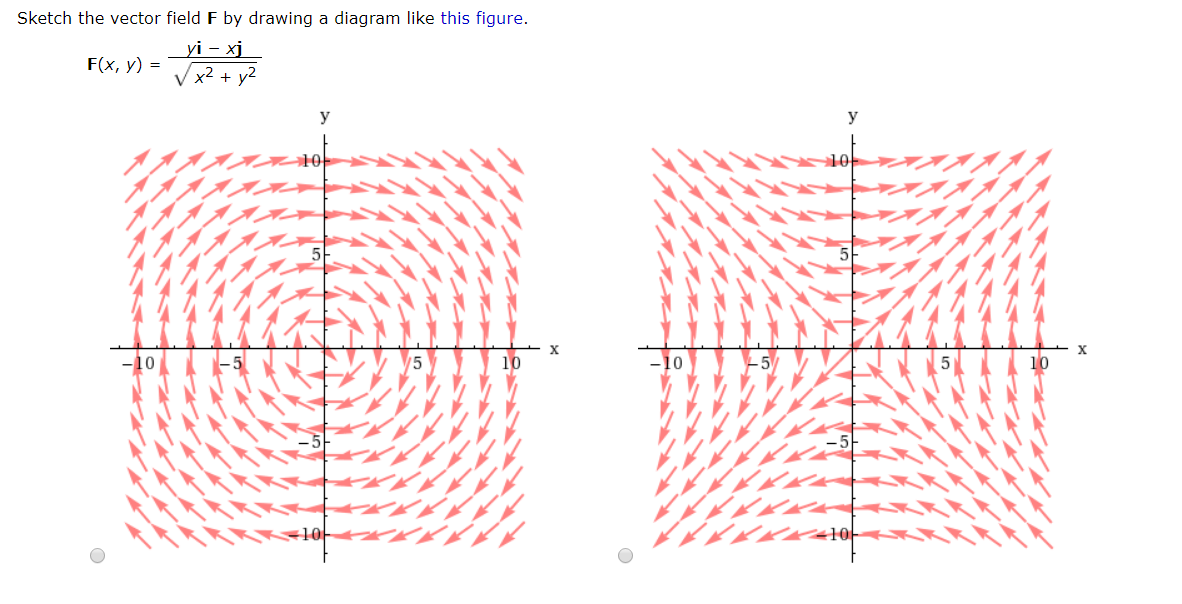
Sketch The Vector Field F By Drawing A Diagram Like This Figure Fx Y Yi

Introduction to Vectors Definitions Components How to Draw a

how to draw E field vectors YouTube

Example of sketching a vector field. YouTube

22+ How To Draw Vector Fields Image Ilutionis
Drawing Vector Field at Explore collection of
![[sketch vector fields] How to go about sketching vector fields? r](http://d2vlcm61l7u1fs.cloudfront.net/media/759/759ef035-9af6-49b5-a983-c08bf40d2c1c/phpwi9YLC.png)
[sketch vector fields] How to go about sketching vector fields? r

HartleyMath Vector Fields

Vector Fields GeoGebra
Use these vectors and sketch some of them on the xyplane to give you
Web The Function P P, Q Q, R R (If It Is Present) Are Sometimes Called Scalar Functions.
Vector Fields And Line Integrals In The Plane.
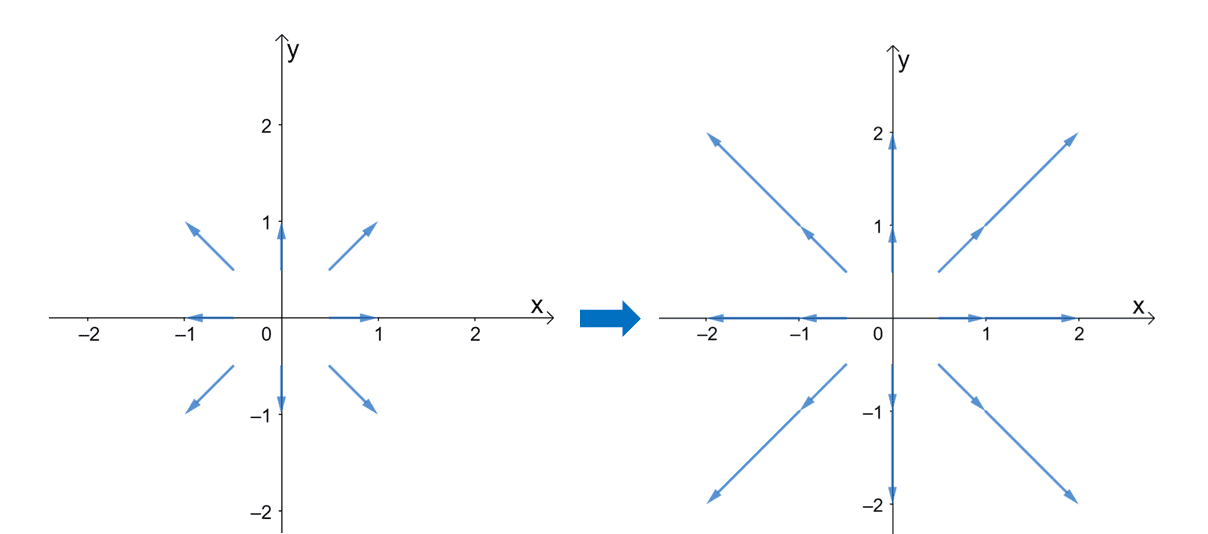
So To Start Off, Let's Take A Very Simple Example, One Where The Vector That Outputs Is.
Web Definition Of Vector Field.
Related Post: